Totzeit-Glied
Inhalt
Totzeit-Glied¶
Totzeit-Glied (T\(_t\)-Glied)¶
Totzeit Glieder der Form
\[
G(s) = e^{-\tau_d s}
\]
lassen sich in Python nicht direkt definieren. Wir können jedoch solche Glieder mit der Padé-Approximation
\[
e^{-\tau_d s} \approx \frac{-\frac{\tau_d}{2}s+1}{+\frac{\tau_d}{2}s+1}
\]
annähern.
import control
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
def check_proper_tf(Gs):
"""check if transferfunction is proper"""
return len(Gs_pade1.num[0][0]) <= len(Gs_pade1.den[0][0])
tdelay = 1
norder = 1
num,den = control.pade(tdelay,norder)
Gs_pade1 = control.tf(num,den)
print(Gs_pade1)
print(check_proper_tf(Gs_pade1))
-s + 2
------
s + 2
True
tdelay = 1
norder = 2
num,den = control.pade(tdelay,norder)
Gs_pade2 = control.tf(num,den)
print(Gs_pade2)
print(check_proper_tf(Gs_pade2))
s^2 - 6 s + 12
--------------
s^2 + 6 s + 12
True
tdelay = 1
norder = 7
num,den = control.pade(tdelay,norder)
Gs_pade3 = control.tf(num,den)
print(Gs_pade3)
print(check_proper_tf(Gs_pade2))
-s^7 + 56 s^6 - 1512 s^5 + 2.52e+04 s^4 - 2.772e+05 s^3 + 1.996e+06 s^2 - 8.649e+06 s + 1.73e+07
------------------------------------------------------------------------------------------------
s^7 + 56 s^6 + 1512 s^5 + 2.52e+04 s^4 + 2.772e+05 s^3 + 1.996e+06 s^2 + 8.649e+06 s + 1.73e+07
True
# step response
t = np.arange(0,2,0.01)
(tout1, yout1) = control.step_response(Gs_pade1,t)
(tout2, yout2) = control.step_response(Gs_pade2,t)
(tout3, yout3) = control.step_response(Gs_pade3,t)
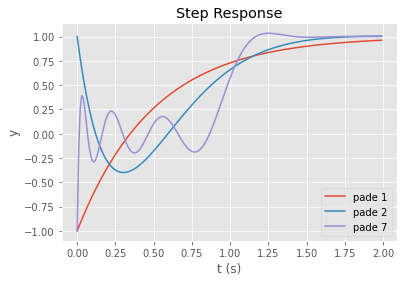
plt.plot(tout1, yout1, label='pade 1')
plt.plot(tout2, yout2, label='pade 2')
plt.plot(tout3, yout3, label='pade 7')
plt.title("Step Response")
plt.ylabel("y")
plt.xlabel("t (s)")
plt.legend()
<matplotlib.legend.Legend at 0x7f0d24c8beb0>