Pandas
Inhalt
Pandas¶
Hier wollen wir nun den Iris Datensatz mit Hilfe von pandas Untersuchen. Dieser Datensatz eignet sich hervorragend um erste Schritte in Pandas zu machen.
# load all modules
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
plt.style.use('ggplot')
import seaborn as sns
Für viele Python-Bibliotheken können wir die Version mit __version__ auslesen.
print(np.__version__)
print(pd.__version__)
print(matplotlib.__version__)
print(sns.__version__)
1.21.2
1.3.3
3.4.3
0.11.2
Python eignet sich hervorragend für die Datenanalyse. Für einen schnellen Start greifen wir auf Datensätze zurück, welche in der Literatur oft besprochen und mit seaborn, sk-learn oder pytorch ausgeliefert werden.
# get all datasets
sns.get_dataset_names()
['anagrams',
'anscombe',
'attention',
'brain_networks',
'car_crashes',
'diamonds',
'dots',
'exercise',
'flights',
'fmri',
'gammas',
'geyser',
'iris',
'mpg',
'penguins',
'planets',
'tips',
'titanic']
Iris Datensatz¶
Einer der bekanntesten Datensätze ist wohl der Iris Datensatz. Oft wird dieser verwendet um Methoden aus dem maschinellen Lernen einzuführen.
'iris' in sns.get_dataset_names()
True
Pandas Grundfunktionen¶
seaborn gibt die eingebauten Datensätze schon als pandas DataFrame aus. Wir sehen wie eng die Bibliotheken numpy, matplotlib, seaborn und pandas miteinander verzahnt sind.
Wir könne also den Iris Datensatz laden.
iris_df = sns.load_dataset("iris")
Es handelt sich um einen neuen Datentyp welcher mit der pandas Bibliothek ausgeliefert wird.
type(iris_df)
pandas.core.frame.DataFrame
Oft ist es hilfreich die größer des DataFrames zu untersuchen.
iris_df.shape
(150, 5)
Eine erste Übersicht bekommen wir mit:
iris_df
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| ... | ... | ... | ... | ... | ... |
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | virginica |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | virginica |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | virginica |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | virginica |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | virginica |
150 rows × 5 columns
Mit head werden die ersten 5 Zeilen eines Datensatzes ausgegeben.
iris_df.head()
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
Die Anzahl der Zeilen lassen mit einem Argument steuern.
iris_df.head(10)
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| 5 | 5.4 | 3.9 | 1.7 | 0.4 | setosa |
| 6 | 4.6 | 3.4 | 1.4 | 0.3 | setosa |
| 7 | 5.0 | 3.4 | 1.5 | 0.2 | setosa |
| 8 | 4.4 | 2.9 | 1.4 | 0.2 | setosa |
| 9 | 4.9 | 3.1 | 1.5 | 0.1 | setosa |
Mit tail() werden die letzten 5 Zeil des DataFrames ausgegeben.
iris_df.tail()
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | virginica |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | virginica |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | virginica |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | virginica |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | virginica |
iris_df.tail(10)
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 140 | 6.7 | 3.1 | 5.6 | 2.4 | virginica |
| 141 | 6.9 | 3.1 | 5.1 | 2.3 | virginica |
| 142 | 5.8 | 2.7 | 5.1 | 1.9 | virginica |
| 143 | 6.8 | 3.2 | 5.9 | 2.3 | virginica |
| 144 | 6.7 | 3.3 | 5.7 | 2.5 | virginica |
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | virginica |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | virginica |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | virginica |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | virginica |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | virginica |
Mit info() bekommt man eine erste Zusammenfassung des Datensatzes. Vor allem sehen wir hier auch die Datentypen. Zum Beispiel können nur für nummerische Datentypen gewisse statische Merkmale berechnet werden.
iris_df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 sepal_length 150 non-null float64
1 sepal_width 150 non-null float64
2 petal_length 150 non-null float64
3 petal_width 150 non-null float64
4 species 150 non-null object
dtypes: float64(4), object(1)
memory usage: 6.0+ KB
Statitische Merkmale¶
Für einige Datensätze ist der Befehl describe() sehr hilfreich. Es werden gewisse statistische Eigenschaften des Datensatzes berechnet.
iris_df.describe()
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| count | 150.000000 | 150.000000 | 150.000000 | 150.000000 |
| mean | 5.843333 | 3.057333 | 3.758000 | 1.199333 |
| std | 0.828066 | 0.435866 | 1.765298 | 0.762238 |
| min | 4.300000 | 2.000000 | 1.000000 | 0.100000 |
| 25% | 5.100000 | 2.800000 | 1.600000 | 0.300000 |
| 50% | 5.800000 | 3.000000 | 4.350000 | 1.300000 |
| 75% | 6.400000 | 3.300000 | 5.100000 | 1.800000 |
| max | 7.900000 | 4.400000 | 6.900000 | 2.500000 |
Solche Merkmale lassen sich auch einfach selbst mit Pandas ermitteln. Dafür selektieren wir nur jene Spalten welche nummerische Werte beinhalten.
cols=['sepal_length','sepal_width','petal_width','petal_width']
Der sample mean ist das arithmetische Mittel
iris_df[cols].mean()
sepal_length 5.843333
sepal_width 3.057333
petal_width 1.199333
petal_width 1.199333
dtype: float64
Das sample median ist der „Mittelpunkt“ eines geordneten Datensatzes.
iris_df[cols].median()
sepal_length 5.8
sepal_width 3.0
petal_width 1.3
petal_width 1.3
dtype: float64
Die Stichprobenvarianz (sample variance) ist ein Maß für die Streuung, ungefähr der durchschnittliche quadrierte Abstand eines Datenpunkts vom arithmetischen Mittelwert (sample mean). Die Standardabweichung (standard deviation) ist die Quadratwurzel aus der Varianz und wird als „durchschnittlicher“ Abstand eines Datenpunkts vom Mittelwert interpretiert.
Stichprobenvarianz (sample variance)
Standardabweichung (standard deviation)
iris_df[cols].var()
sepal_length 0.685694
sepal_width 0.189979
petal_width 0.581006
petal_width 0.581006
dtype: float64
iris_df[cols].std()
sepal_length 0.828066
sepal_width 0.435866
petal_width 0.762238
petal_width 0.762238
dtype: float64
Das \(p\)-te Perzentil ist die Zahl im Datensatz, bei der etwa \(𝑝%\) der Daten kleiner als diese Zahl sind. Diese Zahl wird auch als Quantil bezeichnet
iris_df[cols].quantile(.1) # the 10th percentile
sepal_length 4.8
sepal_width 2.5
petal_width 0.2
petal_width 0.2
Name: 0.1, dtype: float64
iris_df[cols].quantile(.95) # the 95th percentile
sepal_length 7.255
sepal_width 3.800
petal_width 2.300
petal_width 2.300
Name: 0.95, dtype: float64
iris_df[cols].quantile(.75) # commonly known as the third quartile
sepal_length 6.4
sepal_width 3.3
petal_width 1.8
petal_width 1.8
Name: 0.75, dtype: float64
iris_df[cols].quantile(.25) # commonly known as the first quartile
sepal_length 5.1
sepal_width 2.8
petal_width 0.3
petal_width 0.3
Name: 0.25, dtype: float64
Wenn \(Q_i\) das \(i\)-te Quartil bezeichnet, ist der innere Quartilsbereich (IQR=inner-quartile range) die Differenz zwischen dem dritten Quartil und dem ersten Quartil.
iris_df[cols].quantile(.75) - iris_df[cols].quantile(.25)
sepal_length 1.3
sepal_width 0.5
petal_width 1.5
petal_width 1.5
dtype: float64
Weitere wichtige Eigenschaften sind sicher durch das Minimum und das Maximum gegeben.
iris_df[cols].min()
sepal_length 4.3
sepal_width 2.0
petal_width 0.1
petal_width 0.1
dtype: float64
iris_df[cols].max()
sepal_length 7.9
sepal_width 4.4
petal_width 2.5
petal_width 2.5
dtype: float64
Pandas Spalten¶
Manchmal wollen wir aber nur eine Spalte untersuchen. Der Befehl lautet dann:
iris_df['sepal_length'].describe()
count 150.000000
mean 5.843333
std 0.828066
min 4.300000
25% 5.100000
50% 5.800000
75% 6.400000
max 7.900000
Name: sepal_length, dtype: float64
Oder eben als Einzelbefehle:
print("count():", iris_df['sepal_length'].count())
print("mean():",iris_df['sepal_length'].mean())
print("std():",iris_df['sepal_length'].std())
print("min():",iris_df['sepal_length'].min())
print("25%:",iris_df['sepal_length'].quantile(.25))
print("50%:",iris_df['sepal_length'].quantile(.50))
print("75%:",iris_df['sepal_length'].quantile(.75))
print("max():",iris_df['sepal_length'].max())
print("--------------------------------------")
print("var():",iris_df['sepal_length'].var())
print("median():", iris_df['sepal_length'].median())
count(): 150
mean(): 5.843333333333334
std(): 0.828066127977863
min(): 4.3
25%: 5.1
50%: 5.8
75%: 6.4
max(): 7.9
--------------------------------------
var(): 0.6856935123042507
median(): 5.8
Pandas groupby¶
Wie wir schon wissen, repräsentiert dieser Datensatz 3 verschiedene Varianten einer Blume.
iris_df['species'].unique()
array(['setosa', 'versicolor', 'virginica'], dtype=object)
Wir können für jede Variante Statistiken einzeln berechnen. Dazu nutzen wir die Methode groupby.
iris_grps = iris_df.groupby("species")
iris_grps.describe().T
| species | setosa | versicolor | virginica | |
|---|---|---|---|---|
| sepal_length | count | 50.000000 | 50.000000 | 50.000000 |
| mean | 5.006000 | 5.936000 | 6.588000 | |
| std | 0.352490 | 0.516171 | 0.635880 | |
| min | 4.300000 | 4.900000 | 4.900000 | |
| 25% | 4.800000 | 5.600000 | 6.225000 | |
| 50% | 5.000000 | 5.900000 | 6.500000 | |
| 75% | 5.200000 | 6.300000 | 6.900000 | |
| max | 5.800000 | 7.000000 | 7.900000 | |
| sepal_width | count | 50.000000 | 50.000000 | 50.000000 |
| mean | 3.428000 | 2.770000 | 2.974000 | |
| std | 0.379064 | 0.313798 | 0.322497 | |
| min | 2.300000 | 2.000000 | 2.200000 | |
| 25% | 3.200000 | 2.525000 | 2.800000 | |
| 50% | 3.400000 | 2.800000 | 3.000000 | |
| 75% | 3.675000 | 3.000000 | 3.175000 | |
| max | 4.400000 | 3.400000 | 3.800000 | |
| petal_length | count | 50.000000 | 50.000000 | 50.000000 |
| mean | 1.462000 | 4.260000 | 5.552000 | |
| std | 0.173664 | 0.469911 | 0.551895 | |
| min | 1.000000 | 3.000000 | 4.500000 | |
| 25% | 1.400000 | 4.000000 | 5.100000 | |
| 50% | 1.500000 | 4.350000 | 5.550000 | |
| 75% | 1.575000 | 4.600000 | 5.875000 | |
| max | 1.900000 | 5.100000 | 6.900000 | |
| petal_width | count | 50.000000 | 50.000000 | 50.000000 |
| mean | 0.246000 | 1.326000 | 2.026000 | |
| std | 0.105386 | 0.197753 | 0.274650 | |
| min | 0.100000 | 1.000000 | 1.400000 | |
| 25% | 0.200000 | 1.200000 | 1.800000 | |
| 50% | 0.200000 | 1.300000 | 2.000000 | |
| 75% | 0.300000 | 1.500000 | 2.300000 | |
| max | 0.600000 | 1.800000 | 2.500000 |
Die gruppierten Daten können wir erneut statistisch untersuchen. Dadurch können wir Einsichten gewinnen, welche Merkmale für ein Klassifizierung geeignet sein könnten.
iris_grps.mean()
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| species | ||||
| setosa | 5.006 | 3.428 | 1.462 | 0.246 |
| versicolor | 5.936 | 2.770 | 4.260 | 1.326 |
| virginica | 6.588 | 2.974 | 5.552 | 2.026 |
iris_grps.std()
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| species | ||||
| setosa | 0.352490 | 0.379064 | 0.173664 | 0.105386 |
| versicolor | 0.516171 | 0.313798 | 0.469911 | 0.197753 |
| virginica | 0.635880 | 0.322497 | 0.551895 | 0.274650 |
iris_grps.quantile(.75)
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| species | ||||
| setosa | 5.2 | 3.675 | 1.575 | 0.3 |
| versicolor | 6.3 | 3.000 | 4.600 | 1.5 |
| virginica | 6.9 | 3.175 | 5.875 | 2.3 |
iris_grps.quantile(.75) - iris_grps.quantile(.25)
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| species | ||||
| setosa | 0.400 | 0.475 | 0.175 | 0.1 |
| versicolor | 0.700 | 0.475 | 0.600 | 0.3 |
| virginica | 0.675 | 0.375 | 0.775 | 0.5 |
Pandas Diagramme¶
iris_df.plot()
<AxesSubplot:>
iris_df.plot.area(stacked=False)
<AxesSubplot:>
iris_df.plot.area()
<AxesSubplot:>
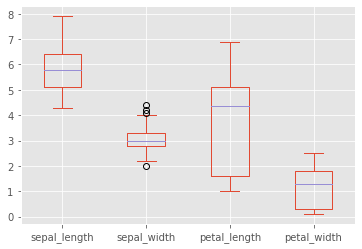
plt.figure(figsize=(10,5))
iris_df.plot.box()
<AxesSubplot:>
<Figure size 720x360 with 0 Axes>
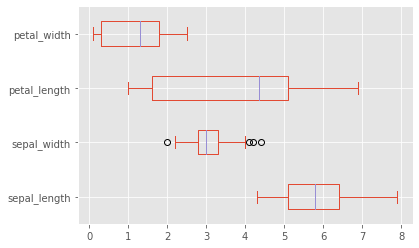
iris_df.plot.box(vert=False)
<AxesSubplot:>
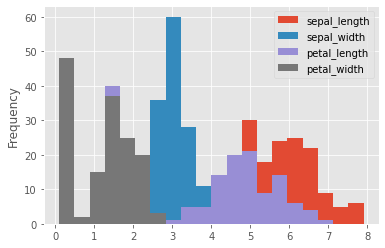
iris_df.plot.hist(bins=20)
<AxesSubplot:ylabel='Frequency'>
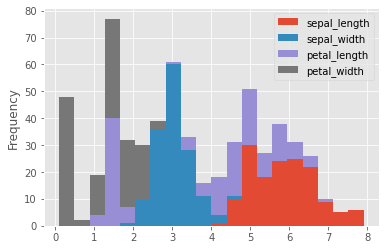
iris_df.plot.hist(stacked=True, bins=20)
<AxesSubplot:ylabel='Frequency'>
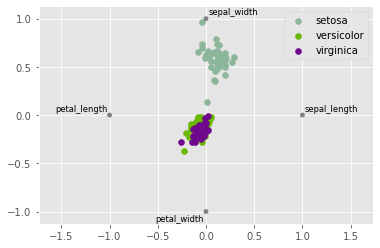
from pandas.plotting import radviz
iris_df.head(1)
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
radviz(iris_df,'species')
<AxesSubplot:>
Scatter¶
name2color = {'setosa':'red','versicolor':'blue','virginica':'green'}
str(iris_df.species.unique())
"['setosa' 'versicolor' 'virginica']"
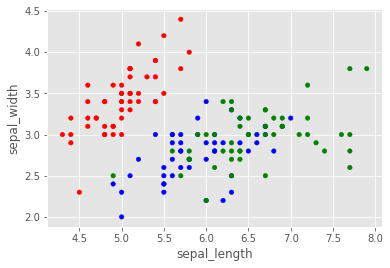
scatter1 = iris_df.plot.scatter(x = 'sepal_length', y = 'sepal_width', c=iris_df['species'].map(name2color))
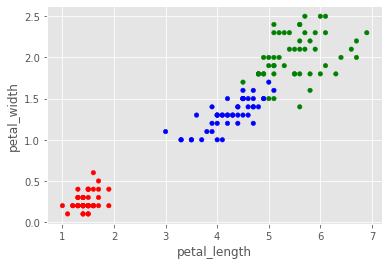
scatter1 = iris_df.plot.scatter(x = 'petal_length', y = 'petal_width', c=iris_df['species'].map(name2color))
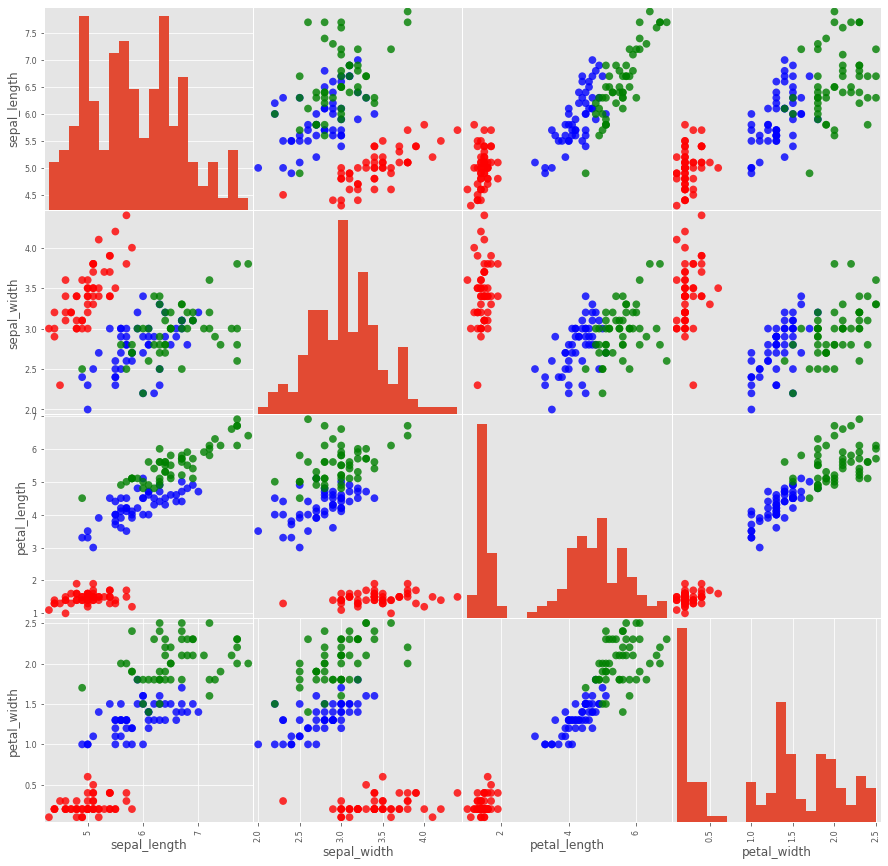
pd.plotting.scatter_matrix(iris_df, c=n2c, figsize=(15, 15), marker='o',
hist_kwds={'bins': 20}, s=60, alpha=.8);
Es gibt noch einige weitere Möglichkeiten Plots in pandas zu erstellen. Eine Beschreibung findet man unter https://pandas.pydata.org/pandas-docs/stable/reference/plotting.html.
Fazit¶
Wir haben einen Datensatz mit pandas untersucht. Für viele Aufgaben in der Datenanalyse ist pandas sehr gut geeignet. Dazu zählen das Einlesen, Bereinigen, Analysieren und Plotten der Daten.
Das Plotten mit den eingebauten pandas Funktionen liefert erste Ergebnisse. Mit seaborn sind oft optische schönere Ergebnisse zu erreichen. Viele Schnittstellen sind unter seaborn einfacher zu handhaben. Auch ist das Hinzufügen von Legenden unter seaborn elegant möglich.
pandas und seaborn laden gemeinsam ein, sich spielerisch der Datenanalyse zu nähern. Einfach einen Datensatz von Internet runterladen und damit spielen.