Inhalt

Kreis mit Kondensator

Kreis mit Kondensator

Kreis mit Kondensator

Wir wollen hier eine weitere Grundschaltung untersuchen. Gegeben sei ein einfacher Kreis mit einer Spannungsquelle und einem Kondensator.

../_images/Kreis_mit_C_3Diagramme.svg

Abb. 14 Kreis mit Kondensator

Analytische Verfahren (reellen Zeitbereich)

Für einen Kondensator

\[ i = C \frac{du}{dt} \]

zwischen Spannung und Strom. Der Strom \(i\) ist also stets gleich der Änderung der Spannung. Bei einem positiven Strom \(i\), nimmt also die Spannung zu. Bei einem negativen Strom \(i\), nimmt die Spannung ab.

In diesem Beispiel sei die Spannung mit

\[ u = \hat{u} \sin \omega t \]

gegeben. Eingesetzt in die obige Gleichung erhalten wir für den Strom

\[ i = C \frac{d u}{d t} = C \frac{ \hat{u} \sin \omega t }{dt} = \omega C \, \hat{u} \cos \omega t. \]

Die Spannung eilt dem Strom um

\[ \varphi = -90^° \]

nach.

Für die Scheitelwerte \(\hat{i}\) und \(\hat{u}\) gilt die Beziehung

\[ \hat{i} = \omega C \hat{u} \]

welche von der Kreisfrequenz \(\omega\) abhängig ist.

import numpy as np
from scipy import signal

import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
from matplotlib import animation, rcParams
plt.style.use('ggplot')
from IPython.display import HTML

#  define parameters
C = 0.5
uh = 1
w = 1

t = np.linspace(0,np.pi*2,180)

u = uh*np.sin(w*t)
i = w*C*uh*np.cos(w*t)

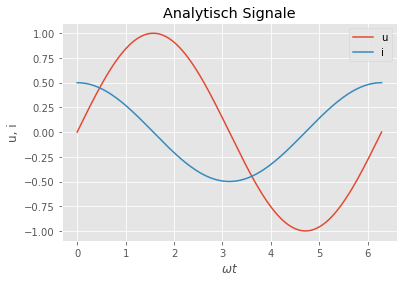
plt.plot(t,u,label='u')
plt.plot(t,i,label='i')
plt.title("Analytisch Signale")
plt.xlabel(r'$\omega t$')
plt.ylabel(r'u, i')
plt.legend()

<matplotlib.legend.Legend at 0x7f9cf5ef0e80>
../_images/wk_C_9_1.png

Komplexe Wechselstromrechnung

Die Wechselstromrechnung vereinfacht diese Rechnung wieder. Durch das Teilen der Gleichung

\[ \hat{i} = \omega C \, \hat{u} \]

mit \(\sqrt{2}\) erhalten wir die Effektivwerte für die Spannung

\[ U = \frac{\hat{u}}{\sqrt{2}} \]

und den Strom

\[ I = \frac{\hat{i}}{\sqrt{2}}. \]

Auch für die Effektivwerte gilt die Gleichung

\[ I = \omega C \, U. \]

Der Vergleich mit dem ohmschen Gesetz \(I=U/R\) zeigt, dass der Ausdruck \(1/(\omega L)\) dem eines Widerstandes entspricht. Wir wollen für ein eigenes Symbol

\[ X_c = - \frac{1}{\omega C} \]

einführen. Diese Größe wird als (kapazitiver) Blindwiderstand oder als Reaktanz bezeichnet. Der Kehrwert

\[ B_C = \omega C = - \frac{1}{X_C} \]

des Blindwiderstands wird als (kapazitiver) Blindleitwert bezeichnet und wird durch positive Zahlenwerte angegeben.

Tipp

Wir geben die Spannung in der Form des sich drehenden komplexen Zeigers

\[ \underline{I} = Ie^{j\omega t} \]

an. Mit dem Zusammenhang

\[ \underline{I} = C \frac{d \underline{U}}{dt} \]

erhalten wir für die Spannung

\[ \underline{I} = j \omega C U e^{j \omega t} = j \omega C \, \underline{U}. \]

Der Ausdruck

\[ jB_C = j\omega C \]

wird als Admittanz des Kondensators bezeichnet. Als Impedanz

\[ jX_C = \frac{1}{jB_C} = \frac{1}{j\omega C} = -j \frac{1}{\omega C} \]

wird der Kehrwert von \(jB_C\) bezeichnet.

U = uh / np.sqrt(2)

Uc = U*np.exp(1j*w*t)
Ic = 1j*w*C*Uc

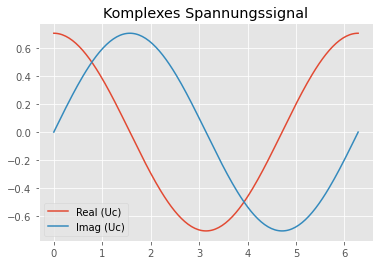
plt.plot(t,Uc.real, label=r'Real (Uc)')
plt.plot(t,Uc.imag, label=r'Imag (Uc)')
plt.title('Komplexes Spannungssignal')
plt.legend()

<matplotlib.legend.Legend at 0x7f9cedd1e6d0>
../_images/wk_C_14_1.png 
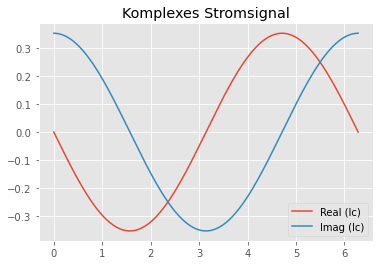
plt.plot(t,Ic.real, label=r'Real (Ic)')
plt.plot(t,Ic.imag, label=r'Imag (Ic)')
plt.title('Komplexes Stromsignal')
plt.legend()

<matplotlib.legend.Legend at 0x7f9ceddec610>
../_images/wk_C_15_1.png 
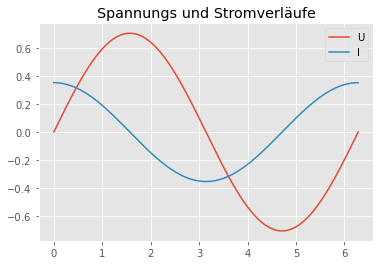
plt.plot(t,Uc.imag, label='U')
plt.plot(t,Ic.imag, label='I')
plt.title('Spannungs und Stromverläufe')
plt.legend()

<matplotlib.legend.Legend at 0x7f9cedcbafd0>
../_images/wk_C_16_1.png

Übertragungsfunktion, Frequenzgang, Bodediagramm

Übertragungsfunktion

Die Übertragungsfunktion für diese Schaltung lautet

\[ G(s) = \frac{I(s)}{U(s)} = \frac{sC}{1} \]

wobei hier die Spannung \(U(s)\) als Eingang und der Strom \(I(s)\) als Ausgang aufgefasst wird. Diese Schaltung ist also ein D-Glied der Form \(\frac{\omega_0 s}{1}\).

Frequenzgang

In der Wechselstromrechnung sind wir nicht an der Übertragungsfunktion \(G(s)\) sondern an dem Frequenzgang \(G(j\omega)\) interessiert. Mit \(\sigma = 0\) in \(s=\sigma+j\omega\) gelingt uns der Übergang von einer Laplace-Übertragungsfunktion \(G(s)\) in den Frequenzgang \(G(j\omega)\) Der Frequenzgang ist nun eine komplexwertige Funktion über die (Kreis-) Frequenz und kann in verschiedenen Schreibweisen dargestellt werden.

Die Schreibweise des Frequenzgangs:

  • mit Real- und Imaginärteil

\[ G(j \omega) = \text{Re} \, G(j \omega) + j \text{Im} \, G(j \omega) \]

  • mit Betrag und Phase

\[\begin{split} \begin{split} G(j \omega) &= \left\vert G(j \omega) \right\vert e^{j \varphi(j \omega )} \\ \left\vert G(j \omega) \right\vert &= \sqrt{(\text{Re} \, G(j \omega))^2+(\text{Im} \, G(j \omega))^2} \qquad \text{Betrag} \\ \varphi(j \omega) &= arctan \left( \frac{\text{Im} \, G(j \omega)}{\text{Re} \, G(j \omega)} \right) \qquad \text{Phase} \end{split} \end{split}\]

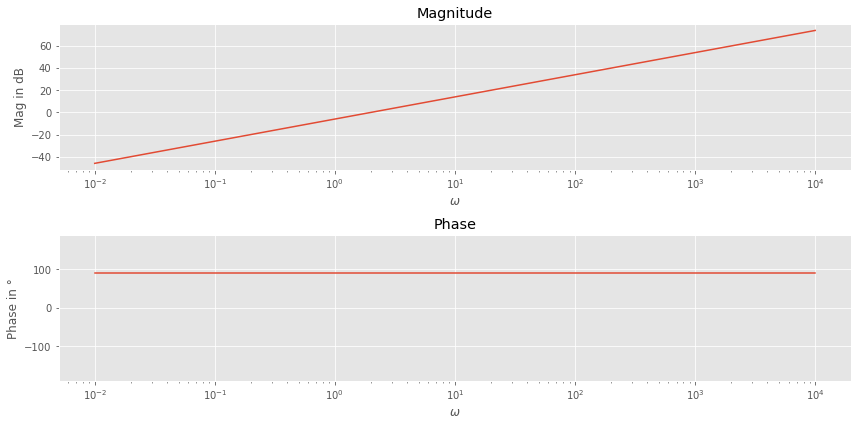
Bodediagramm

Das Bodediagramm ist die graphische Darstellung des Frequenzgangs.

  • x-Achsen: Die Frequenz / Kreisfrequenz wird logarithmisch dargestellt, womit große Frequenzbereiche darstellen lassen.

  • y-Achse: Der Betrag des Frequenzgangs wird in Dezibel (\(20 log(|G|)\)) oder logarithmisch dargestellt. => Amplitudengang

  • y-Achse: Die Phasenverschiebung des Frequenzgangs wird linear aufgetragen. => Phasengang

Wir können die Hilfe für Funktionen einfach mit help(function) aufrufen, Im Falle des scipy Bode Diagramms lautetet es help(signal.bode).

sys = signal.TransferFunction([C, 0], [0, 1])
wbode, mag, phase = signal.bode(sys)

plt.figure(figsize=(12,6))
plt.subplot(211)
plt.semilogx(wbode, mag)    # bode magnitude plot
plt.title('Magnitude')
plt.xlabel(r'$\omega$')
plt.ylabel(r'Mag in dB')
plt.subplot(212)
plt.semilogx(wbode, phase)  # bode phase plot
plt.title('Phase')
plt.xlabel(r'$\omega$')
plt.ylabel(r'Phase in °')
plt.ylim(-190,190)
plt.tight_layout(pad=1.0) # more space between plots
plt.show()
../_images/wk_C_20_0.png

Animation

class PointersSignalsAnimation(animation.TimedAnimation):
    def __init__(self,tc,Uc,Ic):
        fig = plt.figure(figsize=(20,6))
        rcParams.update({'font.size': 16})
        ax1 = fig.add_subplot(1, 2, 1)
        ax2 = fig.add_subplot(1, 2, 2)

        self.t = tc
        self.x1 = Uc.real
        self.y1 = Uc.imag
        
        self.x2 = Ic.real
        self.y2 = Ic.imag

        ax1.set_xlabel('x')
        ax1.set_ylabel('y')
        self.line1Uc, = ax1.plot([], [], '-', lw=2, label='Complex Arrow', color='green')
        self.line1UcReal, = ax1.plot([], [], ':', lw=2, label='Real Part', color='green')
        self.line1UcImag, = ax1.plot([], [], '--o', lw=2, label='Imag Part', color='green')
        self.line1Ic, = ax1.plot([], [], '-', lw=2, label='Complex Arrow', color='red')
        self.line1IcReal, = ax1.plot([], [], ':', lw=2, label='Real Part', color='red')
        self.line1IcImag, = ax1.plot([], [], '--o', lw=2, label='Imag Part', color='red')
        ax1.legend()
        ax1.axis('equal')
        ax1.set(xlim=(-4,4),ylim=(-1, 1))

        ax2.set_xlabel('t')
        ax2.set_ylabel('y')
        self.line2Uc = Line2D([], [], color='green')
        self.line2UcImag, = ax2.plot([], [], '--o', lw=2, color='green', label='U')
        self.line2UcHead = Line2D([], [], color='green', marker='o', markeredgecolor='g')
        self.line2Ic = Line2D([], [], color='red')
        self.line2IcImag, = ax2.plot([], [], '--o', lw=2, color='red', label='I')
        self.line2IcHead = Line2D([], [], color='red', marker='o', markeredgecolor='r')
        ax2.legend()
        ax2.add_line(self.line2Uc)
        ax2.add_line(self.line2UcHead)
        ax2.add_line(self.line2Ic)
        ax2.add_line(self.line2IcHead)
        ax2.set_xlim(0, 2*np.pi)
        ax2.set_ylim(-1, 1)

        animation.TimedAnimation.__init__(self, fig, interval=50, blit=True)
        fig.tight_layout()
        plt.close()

    def _draw_frame(self, framedata):
        i = framedata
        head = i - 1
        
        xc = [0, self.x1[i]]
        yc = [0, self.y1[i]]
        xr = [0, self.x1[i]]
        yr = [0, 0]
        xi = [self.x1[i], self.x1[i]]
        yi = [0, self.y1[i]]

        self.line1Uc.set_data(xc, yc)
        self.line1UcReal.set_data(xr, yr)
        self.line1UcImag.set_data(xi, yi)
        
        x2c = [0, self.x2[i]]
        y2c = [0, self.y2[i]]
        x2r = [0, self.x2[i]]
        y2r = [0, 0]
        x2i = [self.x2[i], self.x2[i]]
        y2i = [0, self.y2[i]]
        
        self.line1Ic.set_data(x2c, y2c)
        self.line1IcReal.set_data(x2r, y2r)
        self.line1IcImag.set_data(x2i, y2i)

        self.line2Uc.set_data(self.t[:i], self.y1[:i])
        x1l = [self.t[head], self.t[head]]
        y1l = [0, self.y1[head]]
        self.line2UcImag.set_data(x1l, y1l)
        self.line2UcHead.set_data(self.t[head], self.y1[head])
        
        self.line2Ic.set_data(self.t[:i], self.y2[:i])
        x2l = [self.t[head], self.t[head]]
        y2l = [0, self.y2[head]]
        self.line2IcImag.set_data(x2l, y2l)
        self.line2IcHead.set_data(self.t[head], self.y2[head])


        self._drawn_artists = [self.line1Uc, self.line1UcReal, self.line1UcImag, self.line1Ic, self.line1IcReal, self.line1IcImag,
                               self.line2Uc, self.line2UcImag, self.line2UcHead, self.line2Ic, self.line2IcImag, self.line2IcHead]

    def new_frame_seq(self):
        return iter(range(self.t.size))

    def _init_draw(self):
        lines = [self.line1Uc, self.line1UcReal, self.line1UcImag, self.line1Ic, self.line1IcReal, self.line1IcImag,
                 self.line2Uc, self.line2UcImag, self.line2UcHead, self.line2Ic, self.line2IcImag, self.line2IcHead]
        for l in lines:
            l.set_data([], [])

ani = PointersSignalsAnimation(t,Uc,Ic)
# ani.save('test_sub.mp4')

HTML(ani.to_jshtml())

Fazit

zurück

Kreis mit Spule

weiter

Regelungstechnik