Inhalt

Kreis mit ohmschem Widerstand

Kreis mit ohmschem Widerstand

Wir wollen hier zeigen, dass Python hervorragend geeignet ist, Wechselstomkreise zu berechnen und zu animieren. Das liegt einerseits an Python selbst, welche den komplexen Zahlen zur Verfügung stellt, als auch an numpy welche Arrays von komplexen Zahlen erlaubt.

Kreis mit ohmschem Widerstand

Wir starten mit dem einfachsten elektrischen Wechselstromkreis, bestehen aus einer Wechselspannungsquelle und einem Widerstand.

../_images/Kreis_mit_R_3Diagramme.svg

Abb. 12 Kreis mit ohmschen Widerstand, (Links: Schaltung, Mitte: Verlauf von Spannung und Strom, Rechts: Zeigerdiagramm)

Analytische Verfahren (reellen Zeitbereich)

Die sinusförmige Versorgungsspannung ist mit

\[ u(t) = \hat{u} \sin \omega t \]

gegeben. Der im Kreis fließende Strom können wir unter Anwendung des ohmschen Gesetzes mit

\[ i(t) = \frac{u}{R} = \frac{\hat{u}}{R} \sin \omega t \]

angeben. Dazu müssen wir jedoch den Wert des Widerstandes \(R\) kennen.

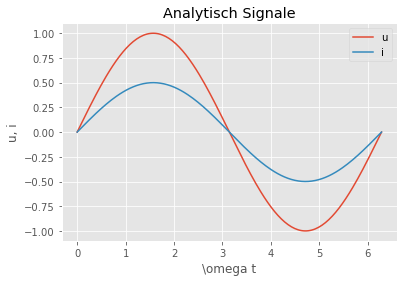
Die Spannung erreicht ihren Scheitelwert bei \(\omega t= \pi/2\) und beträgt \(\hat{u}\). Der Strom erreicht seinen Scheitelwert auch bei \(\omega t= \pi/2\) und beträgt

\[ \hat{i} = \frac{\hat{u}}{R} \]

Die Spannung und der Strom sind also in Phase.

import numpy as np
from scipy import signal

import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
from matplotlib import animation, rcParams
plt.style.use('ggplot')
from IPython.display import HTML

R = 2
uh = 1
w = 1

t = np.linspace(0,np.pi*2,180)

u = uh*np.sin(w*t)
i = u/R

plt.plot(t,u,label='u')
plt.plot(t,i,label='i')
plt.title("Analytisch Signale")
plt.xlabel(r'\omega t')
plt.ylabel(r'u, i')
plt.legend()

<matplotlib.legend.Legend at 0x7f21500e85e0>
../_images/wk_R_10_1.png

Komplexe Wechselstromrechnung

Durch das Teilen der Gleichung

\[ \hat{i} = \frac{\hat{u}}{R} \]

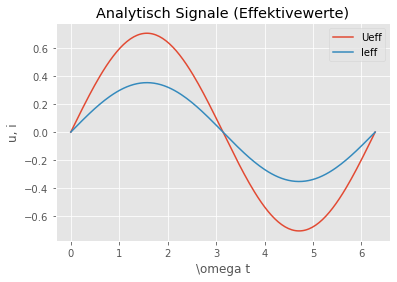
mit \(\sqrt{2}\) erhalten wir die Effektivwerte für die Spannung

\[ U = \frac{\hat{u}}{\sqrt{2}} \]

und den Strom

\[ I = \frac{\hat{i}}{\sqrt{2}}. \]

Tipp

Üblicherweise werden Nenngrößen in der Wechselstromtechnik als Effektivwerte angegeben. Wenn in Mitteleuropa die Angabe von \(230\) V gemacht wird, ist diese eine Effektivwertangabe. Der Scheitelwert liegt dann also bei \(\sqrt{2}*230\) V.

U = uh / np.sqrt(2)

I = U / R

Ueff = U*np.sin(w*t)
Ieff = Ueff / R

plt.plot(t,Ueff,label='Ueff')
plt.plot(t,Ieff,label='Ieff')
plt.title("Analytisch Signale (Effektivewerte)")
plt.xlabel(r'\omega t')
plt.ylabel(r'u, i')
plt.legend()

<matplotlib.legend.Legend at 0x7f2147f11a90>
../_images/wk_R_17_1.png

Bekannterweise lassen sich sinusförmige Wechselgrößen durch komplexe Zeiger darstellen.

Dazu betrachten wir das allgemeine Signal

\[ S_{eff} = S \sin(\omega t + \varphi_u) \]

mit der Amplitude \(S\) und dem Argument \(\omega t + \varphi_s\).

Die komplexe Darstellung des Signals als rotierender Zeiger ist durch den komplexen Ausdruck

\[ \underline{S} = S e^{j(\omega t + \varphi_s)} \]

gegeben. Diese Darstellung wird als Polarform bezeichnet.

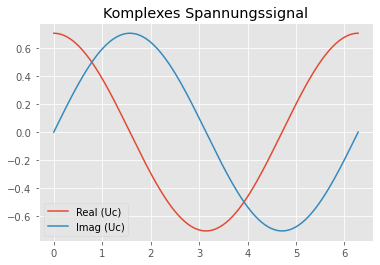
Die Polarform kann in eine Komponentenform

\[ \underline{S} = S \cos(\omega t + \varphi_u) + j S \sin(\omega t + \varphi_u) \]

umgeschrieben werden. Wir sehen, dass das ursprüngliche Signal im Imaginärteil \(Im(S)=S \sin(\omega t + \varphi_u)\) enthalten ist.

Uc = U*np.exp(1j*w*t)

Ic = Uc / R

plt.subplot(121)
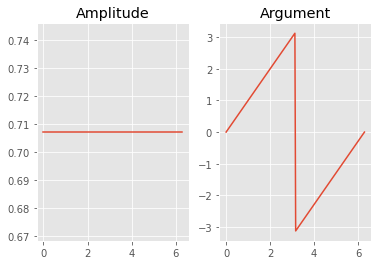
plt.plot(t,np.abs(Uc))
plt.title('Amplitude')
plt.subplot(122)
plt.plot(t,np.angle(Uc))
plt.title('Argument')

Text(0.5, 1.0, 'Argument')
../_images/wk_R_21_1.png 
plt.plot(t,Uc.real, label=r'Real (Uc)')
plt.plot(t,Uc.imag, label=r'Imag (Uc)')
plt.title('Komplexes Spannungssignal')
plt.legend()

<matplotlib.legend.Legend at 0x7f2147f23dc0>
../_images/wk_R_22_1.png 
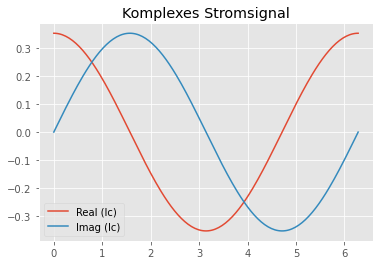
plt.plot(t,Ic.real, label=r'Real (Ic)')
plt.plot(t,Ic.imag, label=r'Imag (Ic)')
plt.title('Komplexes Stromsignal')
plt.legend()

<matplotlib.legend.Legend at 0x7f2147e868e0>
../_images/wk_R_23_1.png 
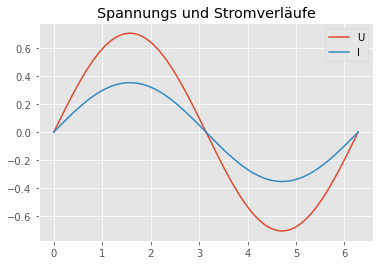
plt.plot(t,Uc.imag, label='U')
plt.plot(t,Ic.imag, label='I')
plt.title('Spannungs und Stromverläufe')
plt.legend()

<matplotlib.legend.Legend at 0x7f2147e2ae80>
../_images/wk_R_24_1.png

Übertragungsfunktion, Frequenzgang, Bodediagramm

Übertragungsfunktion

Die Übertragungsfunktion für diese Schaltung lautet

\[ G(s) = \frac{I(s)}{U(s)} = \frac{1}{R} \]

wobei hier die Spannung \(U(s)\) als Eingang und der Strom \(I(s)\) als Ausgang aufgefasst wird. Diese Schaltung ist also ein P-Glied der Form \(1/R\).

Frequenzgang

In der Wechselstromrechnung sind wir nicht an der Übertragungsfunktion \(G(s)\) sondern an dem Frequenzgang \(G(j\omega)\) interessiert. Mit \(\sigma = 0\) in \(s=\sigma+j\omega\) gelingt uns der Übergang von einer Laplace-Übertragungsfunktion \(G(s)\) in den Frequenzgang \(G(j\omega)\) Der Frequenzgang ist nun eine komplexwertige Funktion über die (Kreis-) Frequenz und kann in verschiedenen Schreibweisen dargestellt werden.

Die Schreibweise des Frequenzgangs:

  • mit Real- und Imaginärteil

\[ G(j \omega) = \text{Re} \, G(j \omega) + j \text{Im} \, G(j \omega) \]

  • mit Betrag und Phase

\[\begin{split} \begin{split} G(j \omega) &= \left\vert G(j \omega) \right\vert e^{j \varphi(j \omega )} \\ \left\vert G(j \omega) \right\vert &= \sqrt{(\text{Re} \, G(j \omega))^2+(\text{Im} \, G(j \omega))^2} \qquad \text{Betrag} \\ \varphi(j \omega) &= arctan \left( \frac{\text{Im} \, G(j \omega)}{\text{Re} \, G(j \omega)} \right) \qquad \text{Phase} \end{split} \end{split}\]

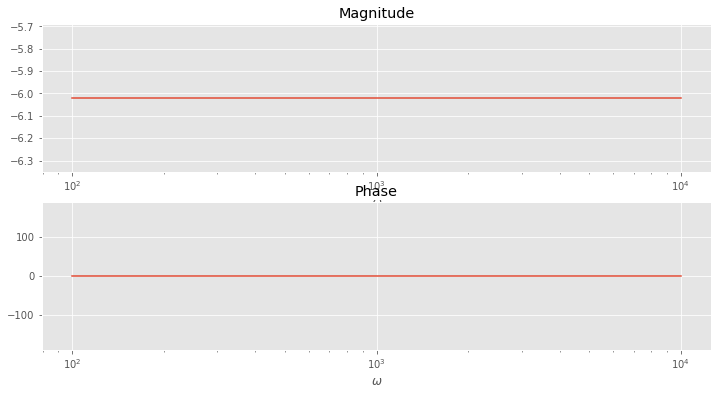
Bodediagramm

Das Bodediagramm ist die graphische Darstellung des Frequenzgangs.

  • x-Achsen: Die Frequenz / Kreisfrequenz wird logarithmisch dargestellt, womit große Frequenzbereiche darstellen lassen.

  • y-Achse: Der Betrag des Frequenzgangs wird in Dezibel (\(20 log(|G|)\)) oder logarithmisch dargestellt. => Amplitudengang

  • y-Achse: Die Phasenverschiebung des Frequenzgangs wird linear aufgetragen. => Phasengang

Wir können die Hilfe für Funktionen einfach mit help(function) aufrufen, Im Falle des scipy Bode Diagramms lautetet es help(signal.bode).

sys = signal.TransferFunction([1/R], [1])
wbode, mag, phase = signal.bode(sys)

plt.figure(figsize=(12,6))
plt.subplot(211)
plt.semilogx(wbode, mag)    # Bode magnitude plot
plt.title('Magnitude')
plt.xlabel(r'$\omega$')
plt.subplot(212)
plt.semilogx(wbode, phase)  # Bode phase plot
plt.title('Phase')
plt.xlabel(r'$\omega$')
plt.ylim(-190,190)
plt.show()
../_images/wk_R_28_0.png

Animation

Python bietet einige Möglichkeiten für Animationen. Animationen können das Verständnis fördern und gerade Schwingungen lassen sich oft gut animieren.

Im Folgenden zeigen wir, wie die Zeigerdarstellung und die analytische Darstellung der komplexen Wechselstromrechnung zusammenhängen.

class PointersSignalsAnimation(animation.TimedAnimation):
    def __init__(self,tc,Uc,Ic):
        fig = plt.figure(figsize=(20,6))
        rcParams.update({'font.size': 16})
        ax1 = fig.add_subplot(1, 2, 1)
        ax2 = fig.add_subplot(1, 2, 2)

        self.t = tc
        self.x1 = Uc.real
        self.y1 = Uc.imag
        
        self.x2 = Ic.real
        self.y2 = Ic.imag

        ax1.set_xlabel('x')
        ax1.set_ylabel('y')
        self.line1Uc, = ax1.plot([], [], '-', lw=2, label='Complex Pointer', color='green')
        self.line1UcReal, = ax1.plot([], [], ':', lw=2, label='Real Part', color='green')
        self.line1UcImag, = ax1.plot([], [], '--o', lw=2, label='Imag Part', color='green')
        self.line1Ic, = ax1.plot([], [], '-', lw=2, label='Complex Pointer', color='red')
        self.line1IcReal, = ax1.plot([], [], ':', lw=2, label='Real Part', color='red')
        self.line1IcImag, = ax1.plot([], [], '--o', lw=2, label='Imag Part', color='red')
        ax1.legend(loc=1)
        ax1.axis('equal')
        ax1.set(xlim=(-4,4),ylim=(-1, 1))

        ax2.set_xlabel('t')
        ax2.set_ylabel('y')
        self.line2Uc = Line2D([], [], color='green')
        self.line2UcImag, = ax2.plot([], [], '--o', lw=2, color='green', label='U')
        self.line2UcHead = Line2D([], [], color='green', marker='o', markeredgecolor='g')
        self.line2Ic = Line2D([], [], color='red')
        self.line2IcImag, = ax2.plot([], [], '--o', lw=2, color='red', label='I')
        self.line2IcHead = Line2D([], [], color='red', marker='o', markeredgecolor='r')
        ax2.legend()
        ax2.add_line(self.line2Uc)
        ax2.add_line(self.line2UcHead)
        ax2.add_line(self.line2Ic)
        ax2.add_line(self.line2IcHead)
        ax2.set_xlim(0, 2*np.pi)
        ax2.set_ylim(-1, 1)

        animation.TimedAnimation.__init__(self, fig, interval=50, blit=True)
        fig.tight_layout()
        plt.close()

    def _draw_frame(self, framedata):
        i = framedata
        head = i - 1
        
        xc = [0, self.x1[i]]
        yc = [0, self.y1[i]]
        xr = [0, self.x1[i]]
        yr = [0, 0]
        xi = [self.x1[i], self.x1[i]]
        yi = [0, self.y1[i]]

        self.line1Uc.set_data(xc, yc)
        self.line1UcReal.set_data(xr, yr)
        self.line1UcImag.set_data(xi, yi)
        
        x2c = [0, self.x2[i]]
        y2c = [0, self.y2[i]]
        x2r = [0, self.x2[i]]
        y2r = [0, 0]
        x2i = [self.x2[i], self.x2[i]]
        y2i = [0, self.y2[i]]
        
        self.line1Ic.set_data(x2c, y2c)
        self.line1IcReal.set_data(x2r, y2r)
        self.line1IcImag.set_data(x2i, y2i)

        self.line2Uc.set_data(self.t[:i], self.y1[:i])
        x1l = [self.t[head], self.t[head]]
        y1l = [0, self.y1[head]]
        self.line2UcImag.set_data(x1l, y1l)
        self.line2UcHead.set_data(self.t[head], self.y1[head])
        
        self.line2Ic.set_data(self.t[:i], self.y2[:i])
        x2l = [self.t[head], self.t[head]]
        y2l = [0, self.y2[head]]
        self.line2IcImag.set_data(x2l, y2l)
        self.line2IcHead.set_data(self.t[head], self.y2[head])


        self._drawn_artists = [self.line1Uc, self.line1UcReal, self.line1UcImag, self.line1Ic, self.line1IcReal, self.line1IcImag,
                               self.line2Uc, self.line2UcImag, self.line2UcHead, self.line2Ic, self.line2IcImag, self.line2IcHead]

    def new_frame_seq(self):
        return iter(range(self.t.size))

    def _init_draw(self):
        lines = [self.line1Uc, self.line1UcReal, self.line1UcImag, self.line1Ic, self.line1IcReal, self.line1IcImag,
                 self.line2Uc, self.line2UcImag, self.line2UcHead, self.line2Ic, self.line2IcImag, self.line2IcHead]
        for l in lines:
            l.set_data([], [])

ani = PointersSignalsAnimation(t,Uc,Ic)
# ani.save('test_sub.mp4')

HTML(ani.to_jshtml())

Fazit

Wir haben den einfachsten Fall eines Wechselstromkreises untersucht und dadurch wichtige Einsichten gewonnen. Durch Diagramme und Animationen kann die Wechselstromrechnung auch gut graphisch verstanden werden.

zurück

Einfache Wechselstromkreise

weiter

Kreis mit Spule