PCA (Toy, Mechanik)¶

Für das Studium der PCA Methode wollen wir als erstes synthetische Daten verwenden. Dieses Setting eignet sich hervorragend für die ersten Versuche.

PCA besteht im Prinzip aus zwei Teilen:

einer Transformation (Koordinatentransformation)
einer Dimensionsreduktion

PCA auf Toy Daten¶

import matplotlib.pyplot as plt
plt.style.use('ggplot')

from sklearn import datasets
from sklearn.decomposition import PCA

import numpy as np

Wir verwenden einen zweidimensionale Gaußverteilung um synthetische Daten zu erzeugen. Dafür müssen wir einen Mittelwert

\[\begin{split} \mu = \begin{bmatrix} \mu_x \\ \mu_y \end{bmatrix} \end{split}\]

und eine Kovarianzmatrix

\[\begin{split} \Sigma = \begin{bmatrix} \Sigma_{xx} & \Sigma_{xy} \\ \Sigma_{yx} & \Sigma_{yy} \end{bmatrix} \end{split}\]

angeben. Eine sinnvolle Angabe für die Kovarianzmatrix ist ohne Erfahrung nicht immer leicht. Für eine einfachere Eingabe verwenden wir einen nützlichen Trick der die Verbindung zur Mechanik schon erahnen lässt.

Wir teilen die Kovarianzmatrix

\[\begin{split} \Sigma = \begin{bmatrix} \Sigma_{xx} & \Sigma_{xy} \\ \Sigma_{yx} & \Sigma_{yy} \end{bmatrix} = \begin{bmatrix} \tilde{\Sigma}_{xx} & 0 \\ 0 & \tilde{\Sigma}_{yy} \end{bmatrix} \begin{bmatrix} cos(q) & -sin(q) \\ sin(q) & cos(q) \end{bmatrix} \end{split}\]

in eine Matrix in der nur die Hauptdiagonalen besetzt werden und einer Rotationsmatrix. Im Prinzip ist die PCA Methode die Umkehrung dieser Idee.

mean = np.array([1, 1]) # Mean
q1 = np.radians(-30)
rot = np.array([[np.cos(q1),np.sin(q1)],[-np.sin(q1),np.cos(q1)]])
cov = np.array([[.01, 0], [0, .5]]) @ rot  # diagonal covariance
X = np.random.multivariate_normal(mean, cov, 200)
plt.scatter(X[:, 0], X[:, 1])
plt.xlim(-3,3)
plt.ylim(-3,3)

/tmp/ipykernel_16172/505636172.py:5: RuntimeWarning: covariance is not positive-semidefinite.
  X = np.random.multivariate_normal(mean, cov, 200)

(-3.0, 3.0)

Tipp

np.random.multivariate_normal benötigt eine positive-semidefinite Matrix. Jedoch scheint dort ein Bug vorhanden. Denn auch wenn wir eine positive-semidefinite Matrix übergeben, gibt numpy eine Warnung aus.

def is_pos_def(x):
    return np.all(np.linalg.eigvals(x) > 0)
is_pos_def(cov)

True

X.shape

(200, 2)

Mit der Hilfe von sklearn lässt sich PCA leicht anwenden. Dazu muss die Anzahl der Komponenten angegeben werden. Zusätzlich lässt sich angeben ob die Daten vorher zentriert werden.

pca = PCA(n_components=2, whiten=True)
pca.fit(X)

PCA(n_components=2, whiten=True)

Transformation¶

Die Transformation können wir nun mit transform durchführen. Damit werden die Daten in dem neuen Koordinatensystem dargestellt und auf die angegeben Komponenten reduziert.

X_pca = pca.transform(X)
X_pca.shape

(200, 2)

plt.scatter(X_pca[:, 0], X_pca[:, 1])
plt.xlim(-3,3)
plt.ylim(-3,3)

(-3.0, 3.0)

def draw_vector(v0, v1, ax=None):
    ax = ax or plt.gca()
    arrowprops=dict(arrowstyle='->',
                    linewidth=2, shrinkA=0, shrinkB=0, color='black')
    ax.annotate('', v1, v0, arrowprops=arrowprops)

# plot data
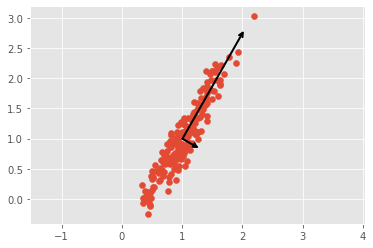
plt.scatter(X[:, 0], X[:, 1])
for length, vector in zip(pca.explained_variance_, pca.components_):
    v = vector * 3 * np.sqrt(length)
    draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal');

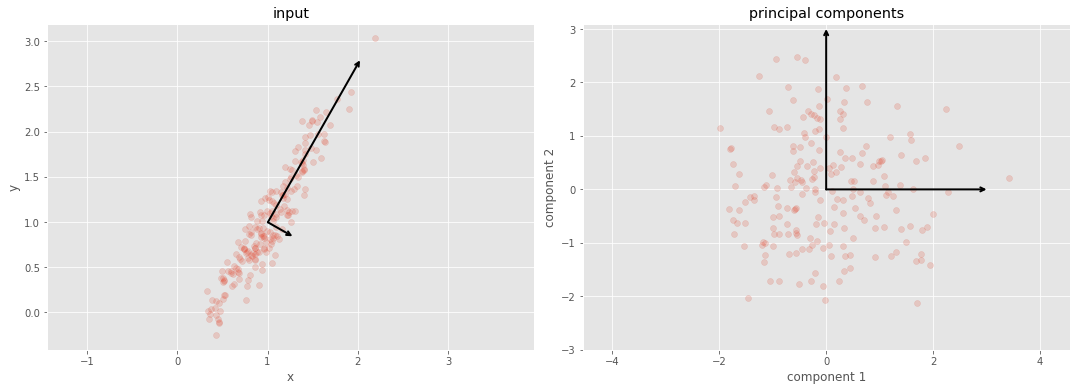
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)

# plot data
ax[0].scatter(X[:, 0], X[:, 1], alpha=0.2)
for length, vector in zip(pca.explained_variance_, pca.components_):
    v = vector * 3 * np.sqrt(length)
    draw_vector(pca.mean_, pca.mean_ + v, ax=ax[0])
ax[0].axis('equal');
ax[0].set(xlabel='x', ylabel='y', title='input')

# plot principal components
X_pca = pca.transform(X)
ax[1].scatter(X_pca[:, 0], X_pca[:, 1], alpha=0.2)
draw_vector([0, 0], [0, 3], ax=ax[1])
draw_vector([0, 0], [3, 0], ax=ax[1])
ax[1].axis('equal')
ax[1].set(xlabel='component 1', ylabel='component 2',
          title='principal components',
          xlim=(-5, 5), ylim=(-3, 3.1))

[Text(0.5, 0, 'component 1'),
 Text(0, 0.5, 'component 2'),
 Text(0.5, 1.0, 'principal components'),
 (-5.0, 5.0),
 (-3.0, 3.1)]

Reduktion¶

Normalerweise wird PCA nicht nur für die Transformation, sondern auch für eine Dimensionsreduktion eingesetzt. Das erreichen wir einfach indem die Anzahl der neunen Komponenten geringer als in den ursprünglichen Daten angeben. Die Daten können nun auf das neue Koordinatensystem transformiert werden.

pca = PCA(n_components=1)
pca.fit(X)
X_pca = pca.transform(X)
print("original shape:   ", X.shape)
print("transformed shape:", X_pca.shape)

original shape:    (200, 2)
transformed shape: (200, 1)

Durch eine Rücktransformation der reduzierten Daten sehen wir das eine Dimension der Daten entfernt worden ist.

X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8)
plt.axis('equal');

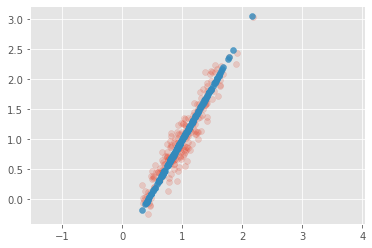
Das hier durchgeführte Beispiel zeigt die Funktionsweise von PCA sehr gut. PCA ist aber vor allem, nützlich wenn der Datensatz sehr viele Dimensionen hat.

PCA und die Hauptachsentransformation¶

Der erste Teil der PCA Methode ist eigentlich nur eine Koordinatentransformation wie sie in der Mathematik oder der Mechanik benötigt wird.

Python für die Kybernetik

PCA (Toy, Mechanik)

Inhalt