PID-Glied
Inhalt
PID-Glied¶
Proportional–Differenzial–Integral–Glied (PID–Glied)¶
\[G(s) = V_P \frac{(1+T_I s)(1+T_D s)}{s (1+T_R s)}\]
Diagramme in Control¶
import control
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
s = control.TransferFunction.s
Vp = 10
Ti = 1/2
Td = 1
Tr = 1/10
Gs = Vp*(1+Ti*s)*(1+Td*s)/(s*(1+Tr*s))
Gs
\[\frac{5 s^2 + 15 s + 10}{0.1 s^2 + s}\]
def check_proper_tf(Gs):
"""check if transferfunction is proper"""
return len(Gs.num[0][0]) <= len(Gs.den[0][0])
check_proper_tf(Gs)
True
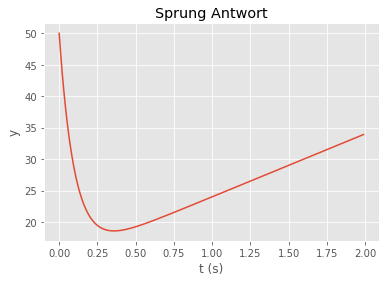
# step response
t = np.arange(0,2,0.01)
(tout, yout) = control.step_response(Gs,t)
plt.plot(tout,yout)
plt.title("Sprung Antwort")
plt.ylabel("y")
plt.xlabel("t (s)")
Text(0.5, 0, 't (s)')
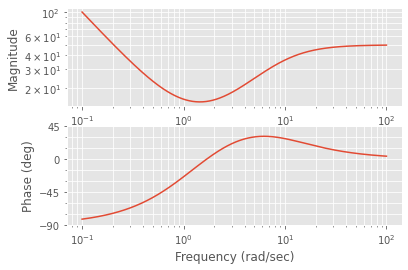
# bode diagram
(mag, phase_rad, w) = control.bode_plot(Gs)
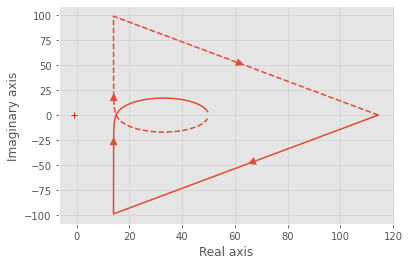
# nyquist plot
res_nyquist = control.nyquist_plot(Gs)
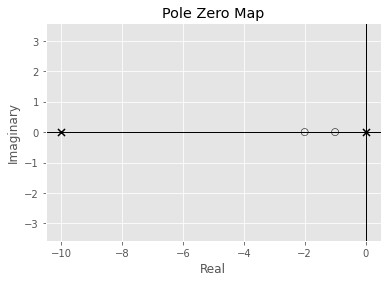
# pole zero map
poles, zeros = control.pzmap(Gs)