PCA (IRIS)
Inhalt
PCA (IRIS)¶
Als zweites Beispiel wollen wir wieder den IRIS Datensatz studieren. Dieser Datensatz gilt auch für die PCA Methode als klassisches Beispiel.
IRIS Datasatz¶
import matplotlib.pyplot as plt
plt.style.use('ggplot')
from sklearn import datasets
from sklearn.decomposition import PCA
Der IRIS Datensatz ist im Python Modul scikit-learn enthalten. Wir erhalten die Eigenschaftsdaten in X und die Labels in y. Mit target_names können wir den Labels Namen zuordnen.
iris = datasets.load_iris()
X = iris.data
y = iris.target
iris.target_names
array(['setosa', 'versicolor', 'virginica'], dtype='<U10')
Das Analysieren der Daten steht immer am Anfang. Mit shape erhalten wir die Dimensionen der Daten. Die Anzahl der Reihen beschreiben wieder die Anzahl der Datenbeispiele und die Spalten die Merkmale der Daten.
print(X.shape)
print(X[:5,:])
(150, 4)
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
Da wir zweidimensionale Daten immer sehr gut darstellen können, wählen wir zwei Komponenten für die Datenreduktion aus und transformieren wir die Daten auf diese.
pca = PCA(n_components=2, whiten=True)
pca.fit(X)
X_pca = pca.transform(X)
X_pca.shape
(150, 2)
Nun werden die Daten in den neuen Komponenten dargestellt.
for i, label in enumerate(iris.target_names):
plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], label=label)
plt.xlabel('first component')
plt.ylabel('second component')
plt.legend()
<matplotlib.legend.Legend at 0x7fb3ada8d220>
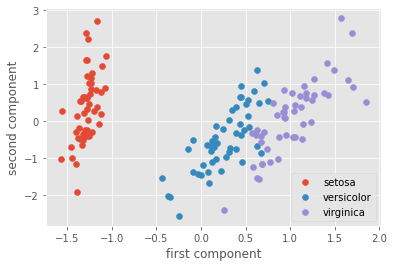
Hier können wir die Klassifikation visuell durchführen.
Fazit¶
PCA ist eine sehr bekannte Methode aus dem maschinellen Lernen und sollte im jeden Fall ausführlich studiert werden. Im Kern nutzt PCA einen Singulärwertzerlegung (SVD). Viele andere Methoden der Modellreduktion basieren ebenfalls auf der Singulärwertzerlegung (SVD). Als Beispiele sollen hier ERA und DMD erwähnt werden.